Question

find the endpoint of the line segment with the given endpoint and midpoint. Endpoint: ( -6,-6) Midpoint: ( -2,0) Endpoint: ( , )

Answer 1

(2, 6)

Step-by-step explanation

To find the endpoint that is missing, we have to state the formula for midpoint between two points:

`(x,\text{ y) = (}(x_1+x_2)/(2),\text{ }(y_1+y_2)/(2))`

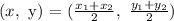
where (x, y) = cordinates of midpoint

(x1, y1) and (x2, y2) are cordinates of the endpoints

So, we have that:

`(-2,\text{ 0) = (}(-6+x_2)/(2),\text{ }(-6+y_2)/(2))`

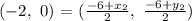
Now, we split the x and y cordinates:

`\begin{gathered} \text{For x:} \\ \Rightarrow\text{ -2 = }(-6+x_2)/(2) \\ Cross-multiply\colon \\ \Rightarrow\text{ -2 }\cdot2=-6+x_2 \\ \Rightarrow-4=-6+x_2 \\ \Rightarrow\text{ }x_2\text{ = -4 + 6} \\ x_2\text{ = 2} \end{gathered}`
`\begin{gathered} \text{For y:} \\ 0\text{ = }(-6+y_2)/(2) \\ \text{Cross multiply:} \\ 0\cdot2=-6+y_2 \\ 0=-6+y_2 \\ \Rightarrow y_2\text{ = 6} \end{gathered}`

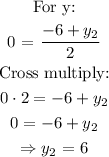
Therefore, the cordinates of the second endpoint is (2, 6)