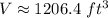1 Answer

John Asmuth · Answer 1 · 2023-01-10T03:18:02+0000

Notice that the figure is composed by a cylinder of height 4ft and diameter 16ft, and a cone with height 6ft and a diameter of 16ft.

Since the radius of a circle is half its diameter, in both cases the radius is equal to 8ft.

Find the volume of each figure and then add them to find the total volume of the composite figure.

Cone:

The volume of a cone with radius r and height h is given by the formula:

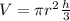
$V=\pi r^2(h)/(3)$

Substitute r=8ft and h=6ft:

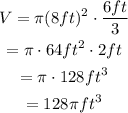
$\begin{gathered} V=\pi(8ft)^2\cdot(6ft)/(3) \\ =\pi\cdot64ft^2\cdot2ft \\ =\pi\cdot128ft^3 \\ =128\pi ft^3 \end{gathered}$

Cylinder:

The volume of a cylinder with radius r and height h is given by the formula:

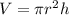
$V=\pi r^2h$

Substitute r=8ft and h=4ft:

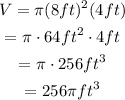
$\begin{gathered} V=\pi(8ft)^2(4ft) \\ =\pi\cdot64ft^2\cdot4ft \\ =\pi\cdot256ft^3 \\ =256\pi ft^3 \end{gathered}$

Composite figure:

Add the volume of the cone and the cylinder to find the volume of the composite figure in terms of π:

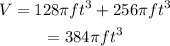
$\begin{gathered} V=128\pi ft^3+256\pi ft^3 \\ =384\pi ft^3 \end{gathered}$

Use the π button on the calculator to find a decimal expression of 384π:

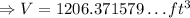
$\Rightarrow V=1206.371579\ldots ft^3$

Therefore, the volume of the composite figure, to the nearest tenth, is:

$V\approx1206.4\text{ }ft^3$

Please log in or register to add a comment.