First, we have to remember the equations involved in the radioactive decomposition:

Where M (t) is the mass through the time, Mo is the initial mass, t is the time and T is the half-life time.
So, in the equation, we know the values of the following variables:
t=24 days
T=8 days
And, what the exercise is asking for is the fraction is the remaining mass, so we can calculate it as follows:
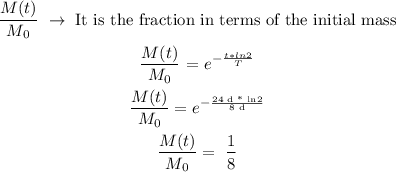
So, the answer will be that the remaining mass of the Isotope 1-131 after 24h is 1/8 of its initial mass.