Question

Use the graph below to write the formula (in factored form) for a polynominal of least degree.If you have a non-integer coefficient then write it as a fraction. Organize factors left to right from smallest zero to largest

Answer 1

`P(x)=(x+3)(x+2)(x-3)(x-4)`

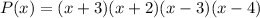
Explanations:

The zeros of the polynomial graph are the points where the polynomial curve cuts the x-axis.

From the given graph, you can see that the curve cuts the x-axis at -3, -2, 3, and 4. Hence the zeros of the polynomial curve will be -3 -2, 3, and 4.

The general polynomial function in "x" is given as:

`P(x)=(x-a)(x-b)(x-c)(x-d)`

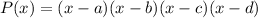
a, b, c and d are the zeros of the polynomial. Substitute the given zeros into the function to have:

`\begin{gathered} P(x)=(x-a)(x-b)(x-c)(x-d) \\ P(x)=(x-(-3))(x-(-2))(x-3)(x-4) \\ P(x)=(x+3)(x+2)(x-3)(x-4) \end{gathered}`

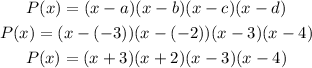
This gives the formula (in factored form) for a polynomial of least degree.