hello
the question given is a right angle triangle and we have to use trigonometric ratios to solve this
SOHCAHTOA
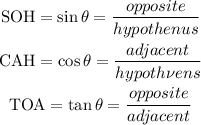
now we can bring in the triangle and see
now we can take each trigonometric ratio and check which one is incorrect
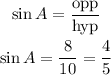
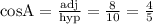
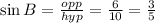
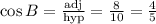
from the calculations above, option A is correct
option B is incorrect
option C is incorrect
option D is correct