We have a situation where the demand of a computer depends on the price.
We know that quantity sold and price have a linear relationship.
We also know that:
- When priced at $1000 (p = 1000), he sold 80 (q = 80).
- When priced at $750 (p = 750), he sold all the stock (q = 100).
We then have two points for the function: (1000, 80) and (750, 100).
With two points we can define a linear function.
We can calculate the slope of the line as:
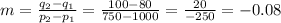
Then, we can write the linear function in point-slope form:
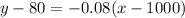
Now, we can calculate the quantity q for p = 1425:

Answer:
The linear model is y = -0.08(x-1000) + 80.
For a price of $1425, it is expected that 46 units are sold.