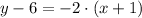Question

Determine the equation of a line in point slope form that passes through (5.-6) and (-1,6)

Answer 1

We need to determine the equation of the line in point-slope form, which is given below:

`y-y_0=m\cdot(x-x_0)`

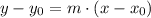
Where (x0, y0) is a known point, and m is the slope of the line. In order to determine the slope, we can use the following expression:

`m=(y_2-y_1)/(x_2-x_1)`

Where (x1, y1) and (x2, y2) are two known points on the line. For our case they are (5, -6) and (-1, 6). Therefore, we have:

`\begin{gathered} m=(6-(-6))/(-1-5) \\ m=(6+6)/(-6) \\ m=(12)/(-6)=-2 \end{gathered}`

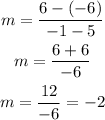
The slope is -2. Now we can determine the equation:

`y-6=-2\cdot(x+1)`