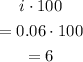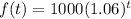
As the initial deposited is $1000
1. In how many years will the money in the acount be 2000
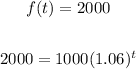
To solve for t:
-Divide both sides of the equation into 1000
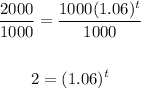
- As:

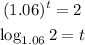
-As:
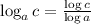
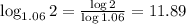
Then, after 11.89 or approximately 12 years the money will be 2000.---------------------------
To find the amount of money after 10 years you substitute the t in the equation for 10 and evaluate the function:
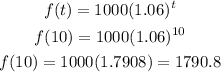
Then, after 10 years the amount of money in the account is $1790.8-----------------------
The general equation for a compounded interest is:

Where C is the initial deposit
i is the interest (in decimal)
As you have:
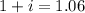
the interest in decimal will be:
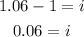
Then, the interest rate is: 6%