Hello there. To solve this question, we'll have to remember some properties about projectile motion and parabolas.
Given the equation for the motion of the projectile:
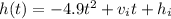
Where h is the height of the object at the time t, vi is the initial velocity and hi is the initial height.
If a cannonball is launched from a height of 58 m above the ground (hi = 58) with an initial velocity of 19.8m/s (vi = 19.8), the equation that models its path is:
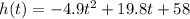
We have to determine the follow:
1. What is the height of the cannonball before it is launched, at t = 0?
By plugging t = 0, the height is the same as the initial height, therefore:
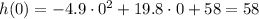
2. When does the cannonball reach it's maximum height?
For this, we need to remember how to find the coordinates of the maximum point of a function. Most specifically, for a parabola, the coordinates of its vertex.
The vertex of a parabola is a point (x, y) such that:
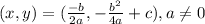
a, b and c are the coefficients of the function f(x) = ax² + bx + c, that is a parabola in the plane.
In this case, a = -4.9, b = 19.8 and c = 58.
We want to determine first when the cannonball will reach its maximum height. For this, we need to find the x-coordinate of the vertex.
Plugging the values into the formula, we get:
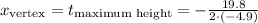
Multiply the values and calculate the fraction
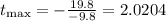
That can be approximated to the nearest whole number as:
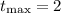
3. The maximum height of the cannonball.
This time, we want the y-coordinate of the vertex. Plugging the coefficients into the formula, we get:
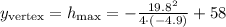
Calculate the square, multiply the values, simplify the fraction and add the values
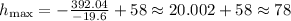
This is the maximum height rounded to the nearest whole number.
4. How long does it take the cannonball to land on the ground?
For this, we have to determine the positive root of the function. Notice the cannonball will land on the ground when h = 0, that only happens one time considering the initial height is not 0.
Therefore we have:
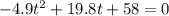
Using the quadratic formula:
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a},a\\e0](https://img.qammunity.org/2023/formulas/mathematics/college/plrj91cdh9gtsfd1b955vcd8ae8pml5fa2.png)
Plugging the values, we get:
![t_(1,2)=\frac{-19.8\pm\sqrt[]{19.8^2-4\cdot(-4.9)\cdot58}}{2\cdot(-4.9)}](https://img.qammunity.org/2023/formulas/mathematics/college/q9u2kiv4cdqxf9dq6y13rybehn5ifh7kba.png)
Calculate the square, multiply the values, add everything in the radical and find the roots:
![t_(1,2)=\frac{-19.8\pm\sqrt[]{392.04+1136.8}}{-9.8}=\frac{-19.8\pm\sqrt[]{1.528,84}}{-9.8}](https://img.qammunity.org/2023/formulas/mathematics/college/zt3qe1ppwp9rvnr7rl5jeur7td45xgrad2.png)
Taking the square root and approximating the values, we get:
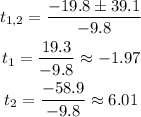
As said earlier, we pick the positive real root: t = 6.01.
Rounding it to the nearest whole number, we get that the cannonball will land on the ground in 6 seconds after the launching.
6. What would be the equation for the cannonball's path if it was launched with the same velocity byt from the ground instead?
Plugging h_i = 0 and the other given data in the formula for the height, we get:
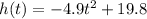
7. Using this new equation, find the new maximum height of the ball and how long did it take to hit the ground?
Plugging the coefficients into the formulas, we get:
Maximum height ==
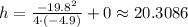
That we can round to the nearest whole number as h = 20.
For the ball to land, we again make:
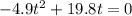
We have two possible solutions:
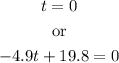
Since it was launched right after t = 0, it couldn't be landing, so the solution we're looking for is given by the equation:
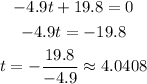
That we round to the nearest whole number as t = 4.