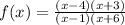Given
Vertical asymptotes at x=1 and x=-6.
x-intercepts at x=4 and x=-3.
Horizontal asymptote at y=3.
To write the rational function.
Now,
Since the vertical asymptotes are at x=1 and x=-6.
Then, the denominator of the rational function is (x-1)(x+6).
Also, the intercepts are at x=4 and x=-3.
Then, the numerator of the rational function is (x-4)(x+3).
That implies,
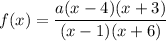
Since the horizontal asymptote y=3.
Then, the function of x approaches infinity.
That is, when x=1, then f(x) will be infinity.
Therefore,