Question

The function y = f (x) is graphed below. What is the average rate of change of the function f (x) on the interval -7 ≤ x ≤ 6?

Answer 1

The average rate of change in a function is determined by :

`=(f(b)-f(a))/(b-a)`

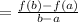
Where :

a = lower limit

b = upper limit

f(a) = value of the function at the lower limit

f(b) = value of the function at the upper limit

From the given problem :

`-7\leqslant x\leqslant6`

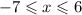
The lower limit is -7 and the upper limit is 6.

So we can say that a = -7 and b = 6

Looking at the figure when x = -7, f(x) = -10

when x = 6, f(x) = -5

Then we can also say that f(a) = -10

and f(b) = -5

Substitute the given values to the formula :

`=(-5-(-10))/(6-(-7))`
`=(5)/(13)`

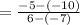
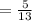
Therefore, the average rate of change is :

`(5)/(13)`