Question

Rapid Rental Car charges a $40 rental fee, $15 for gas, and $0.25 per mile driven. For the same car, Capital Cars charges $45 for rental and gas and $0.35 per mile. write and simplify expression and what is the cost for d miles

Answer 1

The equation for the rental charge includes the following; a fixed rental fee, a charge for gas and charge for miles covered. If the fixed charge for rental is a, the charge for gas is b and the charge per mile is d, then the total rental charge would be;

Cost = a + b + d

For Rapid rental, this becomes

Cost = 40 + 15 + 0.25d

Cost = 55 + 0.25d

However for Capital cars, to rent the same car would cost;

Cost = 45 + 0.35d ( note that Capital charges 45 for rental and gas, so a + b = 45)

The cost per miles for the same car can be expressed as an equation of both expressions. That is;

`\begin{gathered} 55+0.25d=45+0.35d \\ \text{Collect all like terms and you now have} \\ 55-45=0.35d-0.25d \\ 10=0.10d \\ \text{Divide both sides by 0.10} \\ 100=d \end{gathered}`

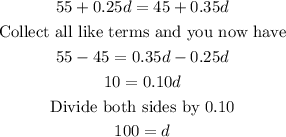
Having calculated the value of d, we can now substitute this into the cost function to get the cost for each rental.

For Rapid Rental, the cost is;

`\begin{gathered} \text{Cost}=55+0.25d \\ \text{Cost}=55+0.25(100) \\ \text{Cost}=55+25 \\ \text{Cost}=80 \end{gathered}`

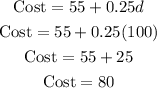
For Capital Cars, the cost is;

`\begin{gathered} \text{Cost}=45+0.35d \\ \text{Cost}=45+0.35(100) \\ \text{Cost}=45+35 \\ \text{Cost}=80 \end{gathered}`

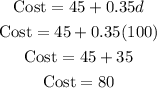
Hence the cost in both rental services is $80