Question 7.
Given the angle:
• (3x + 23)°
,
• 4x
Let's find the measure of angle ABC.
The two given angles are corresponding angles and corresponding angles are congruent.
Thus, we have:
(3x + 23) = 4x
Let's solve for x:
3x + 23 = 4x
Move the term containing x to the left and move the constant to the right:
3x - 4x = -23
-x = -23
Divide both sides by -1:
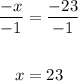
To solve for angle ABC, we have:
m∠ABC = 4x
m∠ABC = 4(23)
m∠ABC = 92°
Therefore, the measure of angle ABC = 92 degrees.
ANSWER:
x = 23°
m∠ABC = 92°