Question

Find the standard devotation of this sample of monthly salaries

Answer 1

The sample standard deviation is calculated as:

`s=\sqrt{\frac{\sum(x_i-\bar{x})^2}{n-1}}`

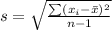
Where:

xi is the value of each sample

x(bar) is the mean of the sample

n is the number of samples

The dataset is 6, 7, 13, 11, 13

First, calculate the mean:

`\bar{x}=(6+7+13+11+13)/(5)=(50)/(5)=10`

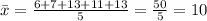
Now compute the differences between each data and the mean:

6 - 10 = -4

7 - 10 = -3

13 - 10 = 3

11 - 10 = 1

13 - 10 = 3

Square each result above:

(6 - 10)^2 = 16

(7 - 10)^2 = 9

(13 - 10)^2 = 9

(11 - 10)^2 = 1

(13 - 10) = 9

Sum the results above:

16 + 9 + 9 + 1 + 9 = 44

Calculate the standard deviation:

`s=\sqrt{(44)/(4)}=√(11)=3.32`

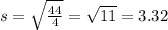
The standard deviation is 3.32