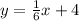Answer
Step-by-step explanation
Given:
The given points are (6, 5) and (12, 6) where slope = 1/6
What to find:
The equation of the line.
Step-by-step solution:
The equation of a line of two points is given as
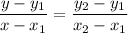
Putting x₁ = 6, y₁ = 5, x₂ = 12, and y₂ = 6, the equation becomes
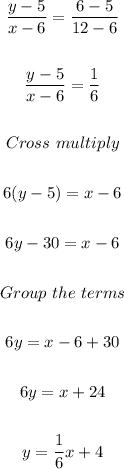
The equation of the line is: