A direct relationship between two variables x and y occur when the variable y grows proportionally with x, you can express a direct relationship as follows:
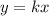
Where k is the constant of proportionality and indicates the increase of y for every unit increase of x.
Relationship A
This is represented by the equation:

This equation shows that every time the variable "x" increases one unit, the variable "y" increases k=9 units. This is a direct relationship between both variables.
Relationship B
To determine the constant proportionality of the relationship shown on the table, you can write the expression that shows a direct relationship for k:
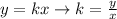
Choose one ordered pair from the table, for example (5,57.5), and replace the values of x and y on the expression to determine the constant of proportionality:
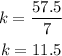
The relationship shown on the table follows a direct relationship with the equation

The rate of change, or constant of proportionality, of the relationship A is k=9, and the rate of change of B is k=11.5, to determine how many units greater the change of rate of B is, with respect to A, you have to calculate the difference between both values:
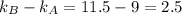
The correct option is B