Question

Calculate the square root of 3249 and 225

Answer 1

- The square root of 3249 is 57.

- The square root of 225 is 15.

Solution

- We are asked to calculate the square root of the two numbers below:

1. 3249

2. 225

- We can do this by finding the prime factorization of both numbers.

`\begin{gathered} 3249=3*3*19*19=3^2*19^2 \\ 225=3*3*5*5=3^2*5^2 \end{gathered}`

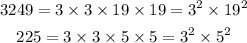
- Since we know that:

`\begin{gathered} \sqrt[]{a^2}=a \\ \text{And}\ldots \\ \sqrt[]{ab}=\sqrt[]{a}*\sqrt[]{b} \end{gathered}`

- We can thus proceed to solve the questions:

Question 1

`\begin{gathered} \sqrt[]{3249}=\sqrt[]{3^2*19^2} \\ we\text{ can rewrite this as:} \\ \sqrt[]{3249}=\sqrt[]{3^2}*\sqrt[]{19^2} \\ \\ \sqrt[]{3249}=3*19 \\ \\ \therefore\sqrt[]{3249}=57 \end{gathered}`

Question 2:

`\begin{gathered} \sqrt[]{225}=\sqrt[]{3^2*5^2} \\ \sqrt[]{225}=\sqrt[]{3^2}*\sqrt[]{5^2} \\ \\ \sqrt[]{225}=3*5=15 \end{gathered}`

Final Answer

- The square root of 3249 is 57.

- The square root of 225 is 15.