The solution of 6x+8=10x-8 is x=4:
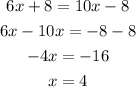
Part A:
We can write:
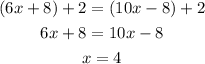
The equation in the second step is the same as the first equation, that has the solution set x=4.
Part B:
We have the first equation squared:
![\begin{gathered} (6x+8)^2=(10x-8)^2 \\ \sqrt[]{(6x+8)^2}=\sqrt[]{(10x-8)^2} \\ |6x+8|=|10x-8| \\ 6x+8=10x-8 \\ x=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9cacfntxhk2hllouyfbitvreol5zz4yvah.png)
Then we have the same equation that we started from.
Part C:
We have a new equation and we have to prove that x=0 is a solution:
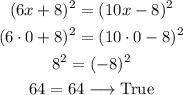
Then, x=0 is a solution.
But if we apply the same to the first equation we get:
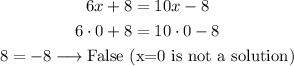
Part D:
When both sides of the equation are squared, both sides will have a positive sign. This does not necesarily happen when the sides are not squared.
For example, the equation we have been working for, when squared, is equal to:
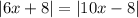
That is why x=0 is a solution for the squared equation but not for the original equation, when both sides end with different sign.