1. To graph this function, we need to find the ordered pairs. We can use the rule for the function to find the corresponding values for y.
We can use the following values of x = { -2, -1, 0, 1, 2, 4, 5}
2. We have a parabola here. The equation is given in the vertex form:
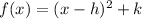
Where, (h, k) is the vertex of the parabola (2, -4).
Then, we have:
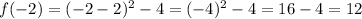
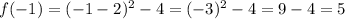
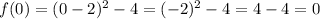
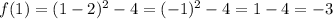

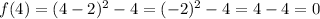
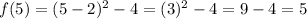
Now, we have the following values to graph the function: (-2, 12), (-1, 5), (0, 0), (1, -3), (2, -4), (4, 0), (5, 5) and we can graph them as follows:
3. We can check that the vertex of the parabola is (2, -4).
4. The line of symmetry is the vertical line that passes through the vertex. In this case, the line of symmetry is x = 2. We can see that at both sides of the line symmetry, the graph is symmetrical:
The green line is the line of symmetry x = 2.
5. The function has a minimum value at the vertex (2, -4). The value for x = 2, and the value for y = -4. Then, the minimum value for the function is (2, -4).
In summary, we have:
• The vertex of the function is (2, -4).
,
• The line of symmetry is x = 2.
,
• The minimum value of the function is (2, -4).