Answer:
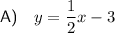
Explanation:
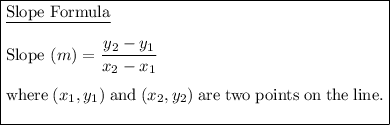
Define two points on the line:
- Let (x₁, y₁) = (0, -3)
- Let (x₂, y₂) = (2, -2)
Substitute the defined points into the formula to find the slope of the line:
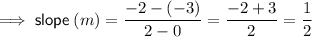
From inspection of the given graph, the line crosses the y-axis at (0, -3). Therefore:

Substitute the found slope and y-intercept into the formula to create an equation of the line:
