Given:
There are given that the y varies jointly as x, z, and w.
And,
The value of x, z, w, and y are:
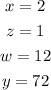
Step-by-step explanation:
According to the above statement, the initial statement is:
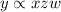
Then,
To convert the equation by multiplying k:
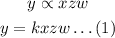
Then,
Put the value of x, y, z, and w into the above equation to find the value of k.
So,
From the equation (1):
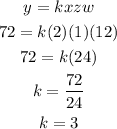
Then,
Put the value of k into the equation (1):
So,
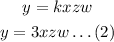
Now,
Put,
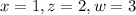
Into the equation (2) to find the value of y.
So,
from the equation (2):
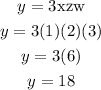
Final answer:
Hence, the value of y is 18.