Question

If you hold a 35.27 cm square plane mirror 60.02 cm from your eyes and can just see the full length of a 4.93 m flag pole behind you, how far are you from the pole?

Answer 1

We are given the following situation:

Where:

`\begin{gathered} h_0=height\text{ of the object} \\ h_i=\text{ height of the image} \\ d_i=\text{ distance to the image} \\ d_0=\text{ distance of the object} \end{gathered}`

We will determine the height of the image by determining the height of the mirror. To do we use the area of the mirror. If the mirror is a square then its area is given by:

`A=h^2`

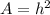
Substituting the value of the area:

`35.27cm^2=h^2`

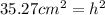
Now, we take the square root to both sides:

`√(35.27cm^2)=h`

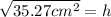
Solving the operations:

`5.9cm=h`

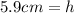
Therefore, the height of the image is 5.9cm.

Now, we determine the magnification using the following formula:

`M=(h_i)/(h_0)`

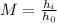
Substituting the values in the formula we get:

`M=(0.059m)/(4.93m)=0.012`

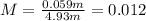
The magnification is also equal to:

`M=-(d_i)/(d_o)`

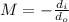
Now, we solve for the distance of the object. First, we multiply both sides by the distance of the object:

`Md_o=-d_i`

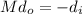
Now, we divide both sides by the magnification:

`d_o=-(d_i)/(M)`

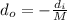
Now, we plug in the values:

`d_o=(-60.02cm)/(0.012)`

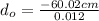
Solving the operations:

`d_o=-5015.23cm`

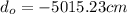
Now, the distance from the observer to the pole is the difference between the distance of the object and the distance of the image:

`d=d_0-d_i`

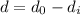
Substituting we get:

`d=5015.23cm-60.02cm=4955.2cm`

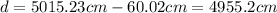
Therefore, the pole is at 4955.2 cm.