First, we need to calculate the growth rate (r). Given that the population triples every month, then if in one month you have 1 rabbit, in the next month you will have 3 rabbits. That is,
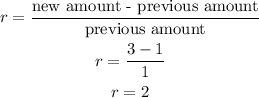
where r is expressed as a decimal.
The exponential growth formula is:
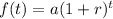
where a is the initial amount, r is the growth rate and t is time
Substituting with a = 35, r = 2, and t = 6, we get:
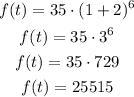
There will be 25515 rabbits in 6 months
Notice that rate, r, was computed considering two consecutive months because time, t, is measured in months