Question

How do I write equations for the piecewise function? For C.

Answer 1

Ok, so

Here we have the following piecewise function.

First, notice that the yellow function is a function which comes from some changes to the function:

`y=\sqrt[]{x}`

If we modify the previous function to get the yellow one, we obtain that the yellow function will be:

`y=-3\sqrt[]{-x-4}-1`

Notice that this function will exist if

`x\leq-4`

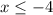
Now, let's see the blue function. As you can see, it has the form of an absolute value function.

Now, our blue function is a function which comes from some changes to the function:

`y=\lvert x\rvert`

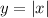
If we modify the previous function to get the blue one, we obtain that the blue function will be:

`y=\lvert(3)/(2)x+3\lvert-1`

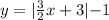
Notice that the function exists if:

`-4Now and finally, the green function has the form of a translated cubic root.<p>Our green function is a function which comes from some changes to the function:</p>[tex]y=\sqrt[3]{x}`

If we modify the previous function to get the green one, we obtain that the green function will be:

`y=2\sqrt[3]{x-6}+4`

As this is a piecewise function, we could write the solution as:

[tex]f(x)=\begin{cases}-3\sqrt[]{-x-4}-1\text{ if }x\leq-4 \\ y=\lvert\frac{3}{2}x+3\lvert-1\text{ if }4