ANSWER
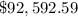
Step-by-step explanation
We want to find how much Juan needs to invest now to meet his target.
To do this, we have to apply the formula for the amount for a quarterly compounded interest:
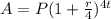
where 4 represents 4 quarters in a year
P = principal or initial amount invested
r = interest rate
A = amount after t years
t = number of years
Therefore, substituting the given values into the equation, we have that:
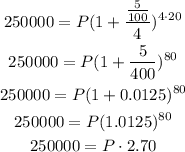
Solve for P by dividing both sides by 2.70:
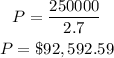
That is the amount that he needs to invest now.