Question

the right pyramid shown has a square base , and its lateral faces are trangles . the surface area of the pyramid is ______ cm2

Answer 1

In order to calculate the surface area of the pyramid, we can calculate the area of the four lateral triangles and the base area.

The lateral faces are triangles with base = 4 cm and height = 8 cm, so we have:

`\begin{gathered} A=(b\cdot h)/(2) \\ A_1=(4\cdot8)/(2)=16\text{ cm}^2 \end{gathered}`

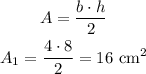
Now, calculating the area of the square base:

`\begin{gathered} A=l^2 \\ A_2=4^2 \\ A_2=16\text{ cm}^2 \end{gathered}`

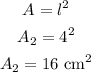
Adding the base area and the four lateral areas, we have:

`\begin{gathered} A=4\cdot A_1+A_2 \\ A=4\cdot16+16 \\ A=64+16 \\ A=80\text{ cm}^2 \end{gathered}`

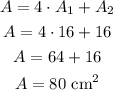
So the surface area of the pyramid is 80 cm².