Question

Pease help me find the least common denominator for this equation

Answer 1

Explanation

We are required to determine the LCD of the given expression.

`(-3)/(x+2)+(5x)/(x-1)-(x+2)/(x^2-3x+2)`

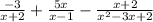
This is achieved thus:

- First, the demominators of the expression given are:

`\begin{gathered} x+2 \\ x-1 \\ x^2-3x+2 \end{gathered}`

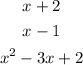
- Next, we factorise the quadratic denominator as follows:

`\begin{gathered} x^2-3x+2 \\ x^2-x-2x+2 \\ (x^2-x)(-2x+2) \\ x(x-1)-2(x-1) \\ (x-1)(x-2) \end{gathered}`

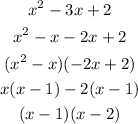
- Finally, the LCD can be calculated as:

Hence, the least common denominator is:

`(x-1)(x-2)(x+2)`

Option C is correct.