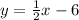The general euqation of the line is

where m is the slope and b tue y-intercep we can calculate each one
Slope
we use two points and the formula
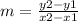
where (x2,y2) is a right point from (x1,y1), so on this case (x2,y2) is (2,5)
now,replacing
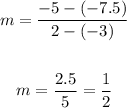
then the slope is 1/2
Y-intercept, b
we replace the value of the slope and a point, i will use (2,-5)
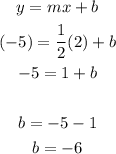
the y-intercept is -6
Equation of the line
replacing the slope an b