a) In 20 years, the account will be worth $13268.58
b) The account will be worth $13350.52
Step-by-step explanation:
a) Principal = P = $6500
rate = r = 3.6% = 0.036
time = t = 20 years
n = number of times it was compounded
n = semi-annually = 2
Using the compound interest formula:
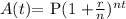
inserting the values in the equation above:
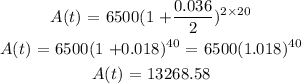
In 20 years, the account will be worth $13268.58
b) n = compunded weekly
n = 52
Principal = P = $6500
rate = r = 3.6% = 0.036
time = t = 20 years
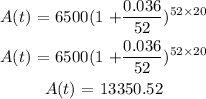
The account will be worth $13350.52