The equation of the given line is,
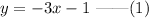
We have to find the equation of a line parallel to y=-3x-1 and passing through the point (x1, y1)=(2, -3).
The general equation of a line is,
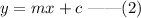
Here, m is the slope of the line.
Comparing equations (1) and (2), we find that the slope of the line y=-3x-1 is m=-3.
The slope of two parallel lines are always equal. Hence, the slope of a line parallel to the line y=-3x-1 is also m=-3.
Now, the formula for the point slope form of the equation of a line can be written as,
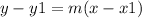
Substitute m=-3, x1=2 and y1=-3 in the above equation to find the equation of a line paralle to y=-3x-1 and passing through point (2, -3) is,
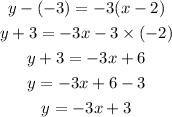
Therefore, the equation of a line paralle to y=-3x-1 and passing through point (2, -3) is y=-3x+3.