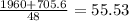Question

compute the monthly payments for an add on interest loan of $1960, with an annual interest rate of 9% and a term of 4 years..

Answer 1

For this case we can use the following formula:

`A=P\cdot(r(1+r)^n)/((1+r)^n-1)`

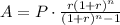
For this case

P= 1960

r= 0,09/12= 0.0075

n= 4*12= 48

Replacing we got:

`A=1960\cdot(0.0075(1+0.0075)^(48))/((1+0.0075)^(48)-1)=48.77`

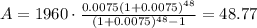
then the answer for this case would be:

48.77$

Solution alternative proposed

`(P+I)/(n)`

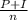
P= 1960 $

I = 0.09*1960*4= 705.6 $

n = 12*4years= 48months

Replacing we got:

`(1960+705.6)/(48)=55.53`