Question

How many boxes of raisin granola bars can inez make if she has 8/3 cups of raisins and each batch required 2/3 cups of raisins

Answer 1

We will have that Inez will be able to make:

`x=(((8)/(3))\cdot(1))/(((2)/(3)))\Rightarrow x=(8\cdot3)/(3\cdot2)\Rightarrow x=(8)/(2)`
`\Rightarrow x=4`

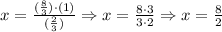
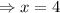
So, Inez will be able to make 4 batches. [Option C]

*** Explanation***

We will have that a linear relationship is given as follows:

*First: We have two values, one we will call "a" and other that we will call "b", "b" is dependent on "a". Now, after that we are given another set of values "c" & "d" that also follow the same rule ("d" is dependent on "c"). Now, we suppose that we know the values for "a", "b" & "c", but not for "d".

We solve for "d" using a ratio, we will have that the ratio for "a" and "b" will be the same ratio than "c" and "d", that is:

`(a)/(b)=(c)/(d)`

And, since we already know the values for "a", "b" & "c" we solve for d, that is:

`(a)/(b)=(c)/(d)\Rightarrow d=(b\cdot c)/(a)`

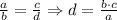
Now, in our case the first set of value ("a" & "b") are "a" = 2/3 cups and "b" = 1 batch; and our second set of values are "c" = 8/3 cups and "d" that is the number of batches we don't know. So, we replae each value in the expression, that is the equivalencies we juststablished:

`d=(b\cdot c)/(a)\Rightarrow d=\frac{(1\text{batch)}\cdot(8/3\text{cups)}}{(2/3\text{cups)}}`
`\Rightarrow d=\frac{(1\text{batch)}((8)/(3))}{((2)/(3))}\Rightarrow d=\frac{(1\text{batch)}\cdot(8\cdot3)}{(3\cdot2)}`

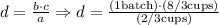
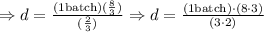
Here we cancel simmilar units and values (In other words, if "cups" divide "cups" they cancel each other out):

`\Rightarrow d=\frac{(1\text{batch)}\cdot8}{2}\Rightarrow d=(1\text{batch)}\cdot4`
`\Rightarrow d=4\text{batches}`

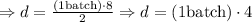
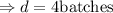
And finally we obtain that the number of batches we would obtain with 8/3 cups is 4 batches.