we are given that a bullet impacts a wooden block that is initially at rest. We are asked to determine the change of momentum of the bullet. To do that we will use the following formula for the change in momentum of an object:
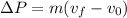
Where:

We need to determine the final velocity of the bullet. To do that we will use the fact that the kinetic energy of the system must be conserved. Therefore, the initial kinetic energy must be equal to the final kinetic energy:
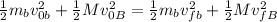
Where:

Now, since the wooden block begins at rest its initial velocity os zero, therefore:
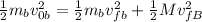
We may cancel out the 1/2:
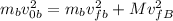
Since the bullet becomes embedded with the block this means that the final velocities are the same, therefore we can use just vf:
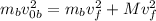
Now we solve for the final velocity first by taking it as a common factor:
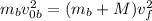
Now we divide both sides by the sum of the masses:
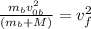
Now we take the square root to both sides:
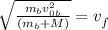
Simplifying we get:
![v^{}_(0b)\sqrt[]{(m_b)/((m_b+M))}=v^{}_f](https://img.qammunity.org/2023/formulas/physics/college/7p8wuun0pzusylrl59d5wday36o9p82vfc.png)
Now we plug in the known values: