Question

Solve the equation below for x using any method: x2 = 8x - 35 - OA. 4+iv 19 O B. x= B. x= – 7; x=5 O c. 4+v 19 OD D. 3 Si

Answer 1

We need to solve the following equation:

`x^2=8x-35`

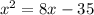
We can start by adding 35 and substracting 8x at both sides of the equation:

`\begin{gathered} x^2=8x-35 \\ x^2-8x+35=8x-35-8x+35 \\ x^2-8x+35=0 \end{gathered}`

So we have a quadratic function equalize to 0 which means that the solutions are the roots of the function. We can find them by using the quadratic solving equation:

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case, a=1, b=-8 and c=35. Then the solving equation looks like:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-(-8)\pm\sqrt[]{(-8)^2-4\cdot35}}{2} \\ x=\frac{8\pm\sqrt[]{64-140}}{2}=\frac{8\pm\sqrt[]{-76}}{2} \\ x=\frac{8\pm\sqrt[]{-76}}{2}=(8)/(2)\pm i\sqrt[]{(76)/(4)} \\ x=4\pm i\sqrt[]{19} \end{gathered}`

Which means that the correct option is A.