Question

Find the solution of the system of equations.6x — 3y=-30 3х — бу = 12

Answer 1

The Solution.

The given system of equations is

`\begin{gathered} 6x-3y=-30\ldots eqn(1) \\ 3x-6y=12\ldots eqn(2) \end{gathered}`

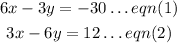
Using the Elimination Method of solving simultaneous equations, we have

`\begin{gathered} 3(6x-3y=-30) \\ 6(3x-6y=12) \end{gathered}`

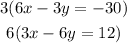
We get

`\begin{gathered} 18x-9y=-90\text{ ..eqn(3)} \\ 18x-36y=72\ldots eqn(4) \end{gathered}`

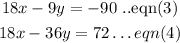
Subtracting eqn(4) from eqn(3), we get

`\begin{gathered} 27y=-162 \\ \text{Dividing both sides by 27, we get} \\ y=-(162)/(27)=-6 \end{gathered}`

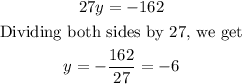
Substituting -6 for y in eqn(2), we get

`\begin{gathered} 3x-6(-6)=12 \\ 3x+36=12 \\ 3x=12-36 \\ 3x=-24 \end{gathered}`

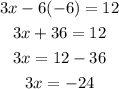
Dividing both sides by 3, we get

`x=-(24)/(3)=-8`

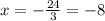
Thus, the correct answer is (-8,-6), that is, x=-8, y=-6