Question

An airplane travels 1498 kilometers against the wind in the 2 hours and 1718 kilometers with the wind in the same amount of time .What is the rate of the plane in still air and what is the rate of the plane in still air and what is the rate of the wind rate of the plane in still air rate of the wind

Answer 1

To find each rate, we have to express the following equations

`\begin{gathered} 2(p-w)=1498 \\ 2(p+w)=1718 \end{gathered}`

The first equation represents the plane against the wind, so we have to subtract.

The second equation represents the plane with the wind, so we have to add.

If we simplify, we get the equations

`\begin{gathered} p-w=(1498)/(2)\rightarrow p-w=749 \\ p+w=(1718)/(2)\rightarrow p+w=859 \end{gathered}`

Then, we combine the equations

`\begin{gathered} p+p+w-w=749+859 \\ 2p=1608 \\ p=(1608)/(2) \\ p=804 \end{gathered}`

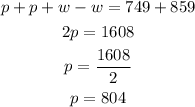
The rate of the plane is 804 km/hr.

Then, we find w

`\begin{gathered} p+w=859 \\ 804+w=859 \\ w=859-804 \\ w=55 \end{gathered}`

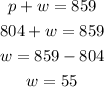
The rate of the wind is 55 km/hr.