Answer:
122°
Step-by-step explanation:
Since the triangle ABC is isosceles, the measures of angles BCA and BCA are the same. So, we can write the following equation:
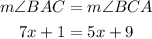
So, solving for x, we get:
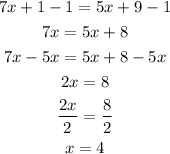
Therefore, the measure of the angle BAC and BCA is:
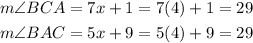
Then, the sum of the interior angles of a triangle is 180, so the vertex angle ABC can be calculated as:
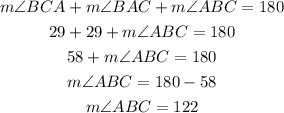
So, the measure of the vertex angle is 122°