SOLUTION
Given the question in the question tab, the following are the solution steps to get the desired probability
Step 1: Write the given parameters
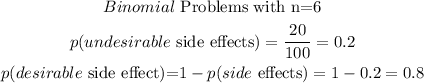
Step 2: State the formula for the Binomial Distribution Model
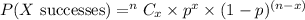
where n is the number of events
x is the required number of event
Step 3: Find the probability of four patients having undesirable side effects among a random sample of six
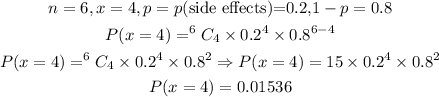
Hence, the probability of four patients having undesirable side effects among a random sample of six is 0.01536