Answer:
-x + 2y = 4
Explanations:
The given function is:
f(x) = -2x + 3
The equation of a line is of the form:
y = mx + c
comparing this equation to f(x) = -2x + 3
m = -2
c = 3
When two lines are perpendicular to each other, the slope of one is the negative inverse of the other.
Since g(x) is perpendicular to f(x), it will have a slope, m = 1/2
Also, g(2) = 3
This means that, the line g(x) passes through the point (2, 3)
The point slope form of the equation of a line is:
y - y₁ = m(x - x₁)
Substituting m = 1/2 , x₁ = 2, and y₁ = 3 into the equation above:
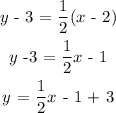
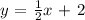
Multiply through by 2
2y = x + 4
-x + 2y = 4