Step-by-step explanation:
Consider the following parental function f(x):

Now, according to the problem, the graph of this function is replaced by the graph of g(x) which is defined as a follows:
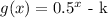
Notice that the transformation that was applied to the function f(x) is a vertical shift of the graph. If k>0, by definition, the vertical shifts of the graphs are:
1) To graph y = f(x) + k, shift the graph of y=f(x) upward k units.
2) To graph y = f(x) - k, shift the graph of y=f(x) downward k units.
According to the second definition, if g(x) is obtained by shifting f(x) down by 3 units, the value of k would be 3 and we obtain:
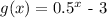
we can conclude that the correct answer is:
Answer:
