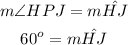Question

Hello I've been having trouble with this problem please help

Answer 1

From the graph, chords HL and HK are equidistance from the center, then they are congruent.

The radius PJ is perpendicular to the chord HK, then PJ bisects HK. This means that:

HN = HK/2

HN = 42/2

HN = 21

PM and PN are congruent, then

PN = PM

PN = 12

In the right triangle PNH, the measure of the angle HPN can be found as follows:

`\begin{gathered} \tan (angle)=\frac{\text{opposite side}}{adjacent\text{ side}} \\ \tan (m\angle HPN)=\frac{\text{HN}}{PN} \\ m\angle HPN=\arctan ((21)/(12)) \\ m\angle HPN\approx60\text{ \degree} \end{gathered}`

The central angle HPJ (which is the same as angle HPN) and the arc HJ are congruent, then:

`\begin{gathered} m\angle HPJ=m\hat{HJ} \\ 60^o=m\hat{HJ} \end{gathered}`