Question

Colbalt-60 has a half-life of 5.27 years. If there was initially 40 grams of the substance, how much is remaining after 15. 81 years?Group of answer choices

Answer 1

Write out the formula for finding half life

`N(t)=N_o((1)/(2))^{(t)/(T)}`

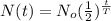
Where N(t) is quantity after that reamains after time t

`\begin{gathered} N_o=\text{original or initial quantity} \\ t=\text{time of decay} \\ T=\text{half life} \end{gathered}`

Define each of the parameters in the question

`\begin{gathered} T=5.27 \\ No=40\text{grams} \\ t=15.81\text{years} \end{gathered}`

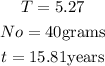
Substitute the given parameters into the half life formula

`\begin{gathered} N(t)=40((1)/(2))^{(15.81)/(5.27)} \\ N(t)=40((1)/(2))^(3.011385) \end{gathered}`
`\begin{gathered} N(t)=40*0.125 \\ N(t)=5g \end{gathered}`

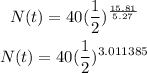
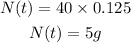
Hence, the remaining substance after 15.81 years is 5g