We are given the graph of a line. We notice that the line goes through the origin, therefore, the equation must be of the following form:

Replacing the point (4, 100) we get:
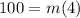
Solving for "m" by dividing by 4 to both sides:
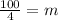
Solving the operation:
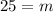
Replacing the value of "m":
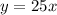
Replacing the value of x = 12:
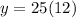
Solving the operation:
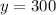
Now for the graph, we use the same general form:

We replace the point (2, 60) we get:
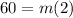
Solving for "m":
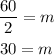
Replacing the value of "m":

Replacing x = 12:
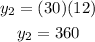
Therefore, the value of "y" is 60 more on the graph in comparison with the table.