The equation of a line with a slope, m, and y-intercept, c is given in slope-intercept form as:

To find the x-intercept, substitute y=0 into the equation:

Since it is given that the line has equal intercepts, equate the y-intercept to the x-intercept:
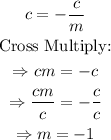
It follows that the slope of the line is -1.
Recall that the equation of a line through (a,b), with slope, m in point-slope form is given as:

Substitute (a,b)=(5/4,-1) and m=-1 into the equation:
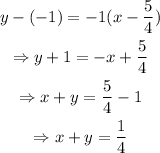
The equation in general form Ax+Bx=C is:
x+y=1/4.