Question

Rational Expressions and Equations Identify any vertical asymptotes or point discontinuities of each function.

Answer 1

To find the vertical asympote or point of dicontinuities

Given function is,

`f(x)=(4x)/(x^2-16)`

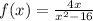
On solving the above equation, we get

`f(x)=(4x)/((x-4)(x+4))`

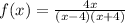
f(x) is not defined when x=4 and x=-4 (that is when denominator tends to zero)

we get,

The point of discontinuity is at x=-4 and x=4

Vertical Asymptote: ertical Asymptote - when x approaches any constant value c, parallel to the y-axis, then the curve goes towards +infinity or – infinity.

we get that,

`\lim _(x\to\pm4)f(x)=\lim _(x\to\pm4)(4x)/(x^2-16)=\pm\infty`

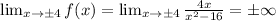
Vertical assymptote of f(x) is x=-4 and x=4