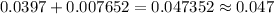Question

Suppose a sample of 1762 floppy disks is drawn. Of these disks, 70 were defective. Using the data construct a 90% confidence interval for the population proportion of discs which are defective. Round your answers to three decimal places

Answer 1

Confidence interval for the following population proportion:

Sample= 1762

Defective disks= 70

Therefore:

`p=(70)/(1762)=0.0397`

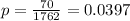
And:

`q=(1-p)=1-0.0397=0.9603`

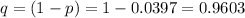
Where q are the disks that are not defective.

The confidence interval is given by:

`CI=Z_c*\sqrt[\placeholder{⬚}]{(p*q)/(n)}`

Where n is the sample= 1762 and Z_c is the z value for a conficence of 90%, Zc= 1.645 . Replacing:

`CI=1.645*\sqrt[\placeholder{⬚}]{(0.0397*0.9603)/(1762)}=0.007652`

Finally, the intervals are given by:

`p\pm CI`

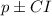
Substituing:

`Intervals=0.0397\pm0.007652`

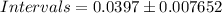
Answer:

Lower Endpoint:

`0.0397-0.007652=0.032048\approx0.032`

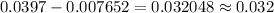
Upper endpoint:

`0.0397+0.007652=0.047352\approx0.047`