Question

Find all solutions of the equation in the interval [0, 2). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)sin x − 5 = cos x − 5

Answer 1

we have the equation

`sinx-5=cosx-5`

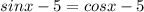
Simplify

`\begin{gathered} s\imaginaryI nx-5=cosx-5 \\ s\imaginaryI nx=cosx-5+5 \\ sinx=cosx \end{gathered}`

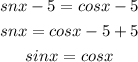
Remember that

The function sine is equal to the function cosine when the angle x is 45 degrees (pi/4)

so

I quadrant ---------> pi/4

II quadrant ----> No solution (different signs)

III quadrant -------> pi+pi/4=5pi/4

IV quadrant ----> No solution (different signs)

therefore

The answer is

x=pi/4,5pi/4