Question

You have 984 grams of a radioactive kind of xenon. If its half-life is 9 hours, how much will be left after 18 hours?

Answer 1

We have to use an exponential decay model to find the mass of the element after 18 hours.

We can model the mass M(t), in grams, in function of t, in hours, as:

`M(t)=a\cdot b^t`

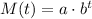
The initial mass, when t = 0 hours, is 984 grams, so we can write:

`\begin{gathered} M(0)=984 \\ a\cdot b^0=984 \\ a=984 \end{gathered}`

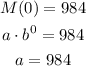
We also know that the half life is 9 hours. This means that the mass at time "t+9" will be half of the mass at time "t".

We can express this as:

`(M(t+9))/(M(t))=(1)/(2)`

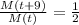
We then can replace and rearrange as:

`\begin{gathered} (984\cdot b^(t+9))/(984\cdot b^t)=(1)/(2) \\ b^(t+9-t)=(1)/(2) \\ b^9=(1)/(2) \\ b=((1)/(2))^{(1)/(9)} \end{gathered}`

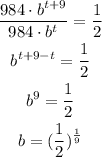
Then, we can write the model for M(t) as:

`M(t)=984\cdot((1)/(2))^{(t)/(9)}`

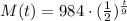
We can calculate the mass after 18 hours as:

`\begin{gathered} M(18)=984\cdot((1)/(2))^{(18)/(9)} \\ M(18)=984\cdot((1)/(2))^2 \\ M(18)=984\cdot(1)/(4) \\ M(18)=246 \end{gathered}`

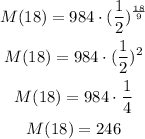
As 18 hours is two times the half-life period, we could have calculated the mass as a double half: 1/2*1/2 = 1/4 of the original mass. But this can only be applied for multiples of 9 hours, the half life period.

However, the model can be used for any value of t.

Answer: the mass after 18 hours is 246 grams.