First, we need to find the equation for both options
x= number of months
y=total cost
The Option 1 equation
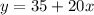
The Option 2
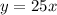
In order to know how many months both options will cost the same.
we need to match both equations
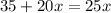
then we need to isolate the x
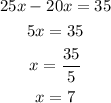
In 7 months the total cost of both options will be the same
In order to know the cost, we substitute the value of x in the first equation
y=35+20(7)
y=35+140
y=175
The cost will be $175