Question

If 500 mg of a radioactive element decays to 350 mg in 24 hours, what is its half-life?____hours

Answer 1

46.64 hours

Explanation:

The amount, A(t) of radioactive material with a half-life of t(0.5) remaining after time t is modeled using the formula below:

`A(t)=A_0\mleft((1)/(2)\mright)^{(t)/(t_((0.5)))}`

• A(t)=quantity of the substance remaining

,

• A(0)=initial quantity of the substance

,

• t=time elapsed

,

• t(0.5)=half life of the substance

In our case:

• A(t)=350 mg

,

• A(0)=500 mg

,

• t = 24 hours

Substitute into the formula above to find the half-life, t(0.5).

`\begin{gathered} 350=500\mleft((1)/(2)\mright)^{(24)/(t_(1/2))} \\ \text{Divide both sides by 500} \\ (350)/(500)=\mleft((1)/(2)\mright)^{(24)/(t_(1/2))} \end{gathered}`

Take the natural logarithm of both sides.

`\begin{gathered} \ln ((350)/(500))=\ln ((1)/(2))^{(24)/(t_(1/2))} \\ (24)/(t(0.5))\ln ((1)/(2))=\ln ((350)/(500)) \end{gathered}`

Divide both sides by ln(1/2).

`\begin{gathered} (24)/(t(0.5))=(\ln((350)/(500)))/(\ln((1)/(2))) \\ \implies(t(0.5))/(24)=(\ln((1)/(2)))/(\ln((350)/(500))) \end{gathered}`

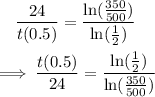
Multiply both sides of the equation by 24.

`\begin{gathered} \implies t(0.5)=24*(\ln((1)/(2)))/(\ln((350)/(500))) \\ t(0.5)=46.64\text{ hours} \end{gathered}`

The half-life of the radioactive element is approximately 46.64 hours.